Note
This document is part of the dune-fem tutorialJupyter notebook (_nb.ipynb) or as Python script (.py)Problem Description
This example considers two-phase porous-media flow. In all that follows, we assume that the flow is immiscible and incompressible with no mass transfer between phases. A detailed description of the mathematical model and parameters can be found [DKKN18]. import sys
[1]:
try:
import dune.femdg
except ImportError:
print("This example needs 'dune.femdg' - skipping")
sys.exit(0)
from matplotlib import pyplot
import sys
import numpy
from ufl import *
from dune.ufl import Space, Constant
import dune.ufl
import dune.fem as fem
from dune.alugrid import aluCubeGrid
from dune.fem.view import adaptiveLeafGridView
from dune.generator import algorithm
from dune.common import FieldVector
from dune.grid import cartesianDomain, Marker
from dune.fem.function import levelFunction, gridFunction
from dune.fem import integrate
from dune.fem.scheme import galerkin
from dune.fem.operator import galerkin as galerkinOp
from dune.fem.space import dglegendrehp, product, finiteVolume
from dune.plotting import plotPointData as plot
from dune.femdg import createOrderRedcution, createLimiter
fem.threading.use = 4
Some parameters
[2]:
maxLevel = 3
maxOrder = 3
dt = 5.
# shorter run time for nightly testing
endTime = 200. if len(sys.argv) > 1 and sys.argv[1] == 'testing' else 800.
coupled = False
# coupled = True
tolerance = 3e-2
penalty = 5 * (maxOrder * ( maxOrder + 1 ))
newtonParameters = {"nonlinear.tolerance": tolerance,
"nonlinear.verbose": "false",
"linear.verbose": "false",
"linear.tolerance": 1e-8,
"linear.reduction": 1e-8}
Defining the model
using a Brooks Corey pressure law
[3]:
def brooksCorey(P,s_n):
s_w = 1-s_n
s_we = (s_w-P.s_wr)/(1.-P.s_wr-P.s_nr)
s_ne = (s_n-P.s_nr)/(1.-P.s_wr-P.s_nr)
if P.useCutOff:
cutOff = lambda a: min_value(max_value(a,0.00001),0.99999)
s_we = cutOff(s_we)
s_ne = cutOff(s_ne)
kr_w = s_we**((2.+3.*P.theta)/P.theta)
kr_n = s_ne**2*(1.-s_we**((2.+P.theta)/P.theta))
p_c = P.pd*s_we**(-1./P.theta)
dp_c = P.pd * (-1./P.theta) * s_we**(-1./P.theta-1.) * (-1./(1.-P.s_wr-P.s_nr))
l_n = kr_n / P.mu_n
l_w = kr_w / P.mu_w
return p_c,dp_c,l_n,l_w
Constants and domain description for anisotropic lens test
[4]:
class AnisotropicLens:
dimWorld = 2
domain = cartesianDomain([0,0.39],[0.9,0.65],[15,4])
x = SpatialCoordinate(dune.ufl.Space(2))
g = [0,]*dimWorld ; g[dimWorld-1] = -9.810 # [m/s^2]
g = as_vector(g)
r_w = 1000. # [Kg/m^3]
mu_w = 1.e-3 # [Kg/m s]
r_n = 1460. # [Kg/m^3]
mu_n = 9.e-4 # [Kg/m s]
lens = lambda x,a,b: (a-b)* \
(conditional(abs(x[1]-0.49)<0.03,1.,0.)* \
conditional(abs(x[0]-0.45)<0.11,1.,0.)) + b
p_c = brooksCorey
Kdiag = lens(x, 6.64*1e-14, 1e-10) # [m^2]
Koff = lens(x, 0,-5e-11) # [m^2]
K = as_matrix( [[Kdiag,Koff],[Koff,Kdiag]] )
Phi = lens(x, 0.39, 0.40) # [-]
s_wr = lens(x, 0.10, 0.12) # [-]
s_nr = lens(x, 0.00, 0.00) # [-]
theta = lens(x, 2.00, 2.70) # [-]
pd = lens(x, 5000., 755.) # [Pa]
#### initial conditions
p_w0 = (0.65-x[1])*9810. # hydrostatic pressure
s_n0 = 0 # fully saturated
# boundary conditions
inflow = conditional(abs(x[0]-0.45)<0.06,1.,0.)* conditional(abs(x[1]-0.65)<1e-8,1.,0.)
J_n = -5.137*1e-5
J_w = 1e-20
dirichlet = conditional(abs(x[0])<1e-8,1.,0.) + conditional(abs(x[0]-0.9)<1e-8,1.,0.)
p_wD = p_w0
s_nD = s_n0
q_n = 0
q_w = 0
useCutOff = False
P = AnisotropicLens()
Setup grid, discrete spaces and functions
[5]:
grid = adaptiveLeafGridView( aluCubeGrid( P.domain, dimgrid=2) )
if coupled:
spc = dglegendrehp(grid, dimRange=2, order=maxOrder)
else:
spc1 = dglegendrehp(grid, dimRange=1, order=maxOrder)
spc = product( spc1,spc1, components=["p","s"] )
solution = spc.function(name="solution")
solution_old = spc.function(name="solution_old")
sol_pm1 = spc.function(name="sol_pm1")
intermediate = spc.function(name="iterate")
persistentDF = [solution,solution_old,intermediate]
fvspc = finiteVolume( grid, dimRange=1)
estimate = fvspc.function(name="estimate")
estimate_pm1 = fvspc.function(name="estimate-pm1")
[6]:
uflSpace = Space((P.dimWorld,P.dimWorld),2)
u = TrialFunction(uflSpace)
v = TestFunction(uflSpace)
x = SpatialCoordinate(uflSpace)
tau = Constant(dt, name="timeStep")
beta = Constant(penalty, name="penalty")
p_w = u[0]
s_n = u[1]
p_c,dp_c,l_n,l_w = P.p_c(s_n=intermediate[1])
Bulk terms
[7]:
dBulk_p = P.K*( (l_n+l_w)*grad(p_w) + l_n*dp_c*grad(s_n) )
dBulk_p += -P.K*( (P.r_n*l_n+P.r_w*l_w)*P.g )
bulk_p = -(P.q_w+P.q_n)
dBulk_s = P.K*l_n*dp_c*grad(s_n)
dBulk_s += P.K*l_n*(grad(p_w)-P.r_n*P.g)
bulk_s = -P.q_n
Boundary and initial conditions
[8]:
p_D, s_D = P.p_wD, P.s_nD,
p_N, s_N = P.J_w+P.J_n, P.J_n
p_0, s_0 = P.p_w0, P.s_n0
Bulk integrals
[9]:
form_p = ( inner(dBulk_p,grad(v[0])) + bulk_p*v[0] ) * dx
form_s = ( inner(dBulk_s,grad(v[1])) + bulk_s*v[1] ) * dx
Boundary fluxes
[10]:
form_p += p_N * v[0] * P.inflow * ds
form_s += s_N * v[1] * P.inflow * ds
DG terms
[11]:
def sMax(a): return max_value(a('+'), a('-'))
n = FacetNormal(uflSpace)
hT = MaxCellEdgeLength(uflSpace)
he = avg( CellVolume(uflSpace) ) / FacetArea(uflSpace)
heBnd = CellVolume(uflSpace) / FacetArea(uflSpace)
k = dot(P.K*n,n)
lambdaMax = k('+')*k('-')/avg(k)
def wavg(z): return (k('-')*z('+')+k('+')*z('-'))/(k('+')+k('-'))
Penalty terms (including dirichlet boundary treatment)
[12]:
p_c0,dp_c0,l_n0,l_w0 = P.p_c(0.5)
penalty_p = [beta*lambdaMax*sMax(l_n0+l_w0),
beta*k*(l_n0+l_w0)]
penalty_s = [beta*lambdaMax*sMax(l_n0*dp_c0),
beta*k*(l_n0*dp_c0)]
form_p += penalty_p[0]/he * jump(u[0])*jump(v[0]) * dS
form_s += penalty_s[0]/he * jump(u[1])*jump(v[1]) * dS
form_p += penalty_p[1]/heBnd * (u[0]-p_D) * v[0] * P.dirichlet * ds
form_s += penalty_s[1]/heBnd * (u[1]-s_D) * v[1] * P.dirichlet * ds
Consistency terms
[13]:
form_p -= inner(wavg(dBulk_p),n('+')) * jump(v[0]) * dS
form_s -= inner(wavg(dBulk_s),n('+')) * jump(v[1]) * dS
form_p -= inner(dBulk_p,n) * v[0] * P.dirichlet * ds
form_s -= inner(dBulk_s,n) * v[1] * P.dirichlet * ds
Time discretization
[14]:
form_s = P.Phi*(u[1]-solution_old[1])*v[1] * dx + tau*form_s
Stabilization (Limiter)
[15]:
limiter = createLimiter( spc, bounds=(None, (1e-12, 1.)), limiter="scaling" )
tmp = solution.copy()
def limit(target):
tmp.assign(target)
limiter(tmp,target)
Time stepping Converting UFL forms to scheme
[16]:
if coupled:
form = form_s + form_p
scheme = galerkin( form == 0, spc, ("suitesparse","umfpack"), parameters=newtonParameters)
else:
uflSpace1 = Space((P.dimWorld,P.dimWorld),1)
u1 = TrialFunction(uflSpace1)
v1 = TestFunction(uflSpace1)
form_p = replace(form_p, { u:as_vector([u1[0],intermediate.s[0]]),
v:as_vector([v1[0],0.]) } )
form_s = replace(form_s, { u:as_vector([solution[0],u1[0]]),
intermediate:as_vector([solution[0],intermediate[1]]),
v:as_vector([0.,v1[0]]) } )
form = [form_p,form_s]
tpModel = [form[0] == 0,
form[1] == 0]
# tpModel[0].penalty = penalty
# tpModel[1].penalty = penalty
# tpModel[1].timeStep = dt
scheme = [galerkin( m, s, ("suitesparse","umfpack"),
parameters=newtonParameters) for m,s in zip(tpModel,spc.subSpaces)]
Stopping condition for iterative approaches
[17]:
def errorMeasure(w,dw):
rel = integrate([w[1]**2,dw[1]**2], order=5, gridView=grid)
return numpy.sqrt(rel[1]) < tolerance * numpy.sqrt(rel[0])
Iterative schemes (iterative or impes-iterative)
[18]:
def step():
n = 0
solution_old.assign(solution)
while True:
intermediate.assign(solution)
if coupled:
scheme.solve(target=solution)
else:
scheme[0].solve(target=solution.p)
scheme[1].solve(target=solution.s)
limit(solution)
n += 1
# print("step",n,flush=True)
if errorMeasure(solution,solution-intermediate) or n==20:
break
HP Adpativity
Setting up residual indicator
[19]:
uflSpace0 = Space((P.dimWorld,P.dimWorld),1)
v0 = TestFunction(uflSpace0)
Rvol = P.Phi*(u[1]-solution_old[1])/tau - div(dBulk_s) - bulk_s
estimator = hT**2 * Rvol**2 * v0[0] * dx + he * inner(jump(dBulk_s), n('+'))**2 * avg(v0[0]) * dS + heBnd * (s_N + inner(dBulk_s,n))**2 * v0[0] * P.inflow * ds + penalty_s[0]**2/he * jump(u[1])**2 * avg(v0[0]) * dS + penalty_s[1]**2/heBnd * (s_D - u[1])**2 * v0[0] * P.dirichlet * ds
estimator = replace(estimator, {intermediate:u})
estimator = galerkinOp( estimator, spc, fvspc)
Marker for grid adaptivity (h)
[20]:
hTol = 1e-16 # changed later
def markh(element):
center = element.geometry.referenceElement.center
eta = estimate.localFunction(element).evaluate(center)[0]
if eta > hTol and element.level < maxLevel:
return Marker.refine
elif eta < 0.01*hTol:
return Marker.coarsen
else:
return Marker.keep
Marker for space adaptivity (p)
[21]:
pTol = 1e-16
def markp(element):
center = element.geometry.referenceElement.center
r = estimate.localFunction(element).evaluate(center)[0]
r_p1 = estimate_pm1.localFunction(element).evaluate(center)[0]
eta = abs(r-r_p1)
polorder = spc.localOrder(element)
if eta < pTol:
return polorder-1 if polorder > 1 else polorder
elif eta > 100.*pTol:
return polorder+1 if polorder < maxOrder else polorder
else:
return polorder
Operator for projecting into space with a reduced order on every element
[22]:
orderreduce = createOrderRedcution( spc )
Main program
Pre adapt the grid
[23]:
hgrid = grid.hierarchicalGrid
hgrid.globalRefine(1)
for i in range(maxLevel):
print("pre adaptive (",i,"): ",grid.size(0),end="\n")
solution.interpolate( as_vector([p_0,s_0]) )
limit(solution)
step()
estimator(solution, estimate)
hgrid.mark(markh)
fem.adapt(persistentDF)
print("final pre adaptive (",i,"): ",dt,grid.size(0),end="\n")
pre adaptive ( 0 ): 240
pre adaptive ( 1 ): 231
pre adaptive ( 2 ): 363
final pre adaptive ( 2 ): 5.0 273
Define the constant for the h adaptivity
[24]:
solution.interpolate( as_vector([p_0,s_0]) )
limit(solution)
estimator(solution, estimate)
timeTol = sum(estimate.dofVector) / endTime
print('Using timeTol = ',timeTol, end='\n')
Using timeTol = 3.216131221875019e-15
Time loop
[25]:
t = 0
saveStep = 0
while t < endTime:
step()
# h adaptivity
hTol = timeTol * dt / grid.size(0)
estimator(solution, estimate)
hgrid.mark(markh)
fem.adapt(persistentDF)
# p adaptivity
estimator(solution, estimate)
orderreduce(solution,sol_pm1)
estimator(sol_pm1, estimate_pm1)
fem.spaceAdapt(markp, persistentDF)
t += dt
if t>=saveStep:
print(f"t = {t:7.2f}, size = {grid.size(0):5}, est = {sum(estimate.dofVector):.4e}, hTol = {hTol}", flush=True)# timestep",flush=True)
plot(solution[1],figsize=(15,4))
saveStep += 100
t = 5.00, size = 240, est = 0.0000e+00, hTol = 5.890350223214321e-17
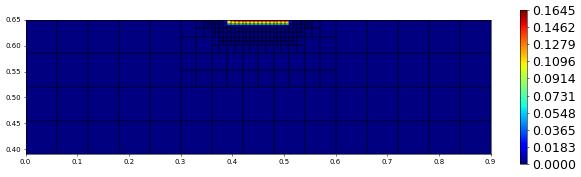
t = 100.00, size = 363, est = 0.0000e+00, hTol = 4.46684891927086e-17
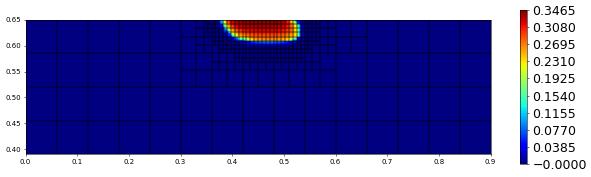
t = 200.00, size = 498, est = 0.0000e+00, hTol = 3.248617395833353e-17

t = 300.00, size = 582, est = 0.0000e+00, hTol = 2.748830104166683e-17
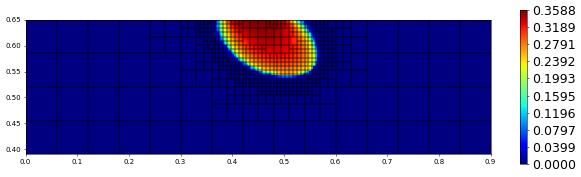
t = 400.00, size = 669, est = 0.0000e+00, hTol = 2.4145129293356e-17

t = 500.00, size = 774, est = 0.0000e+00, hTol = 2.0856882113326973e-17
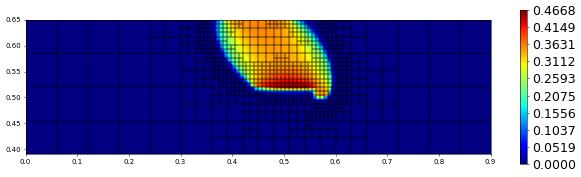
t = 600.00, size = 885, est = 0.0000e+00, hTol = 1.8232036405187182e-17
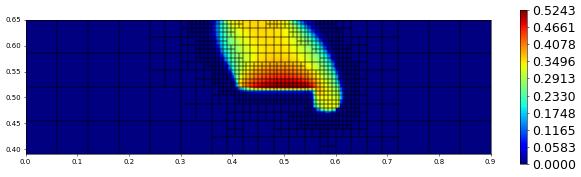
t = 700.00, size = 1017, est = 0.0000e+00, hTol = 1.585863521634625e-17
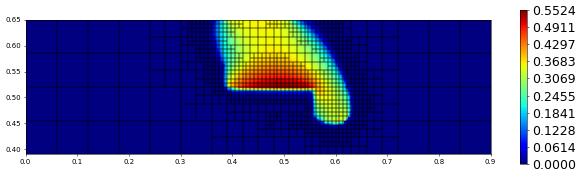
t = 800.00, size = 1134, est = 0.0000e+00, hTol = 1.4255900806183596e-17
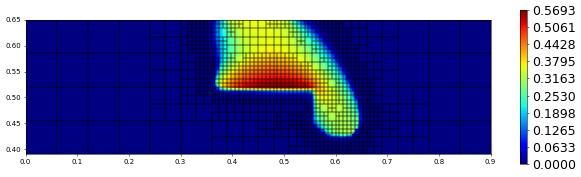
Postprocessing Show solution along a given line
[26]:
x0 = FieldVector([0.25, 0.65])
x1 = FieldVector([0.775, 0.39])
p,v = algorithm.run('sample', 'utility.hh', solution, x0, x1, 1000)
x = numpy.zeros(len(p))
y = numpy.zeros(len(p))
l = (x1-x0).two_norm
for i in range(len(x)):
x[i] = (p[i]-x0).two_norm / l
y[i] = v[i][1]
pyplot.plot(x,y)
[26]:
[<matplotlib.lines.Line2D at 0x7fb670722090>]
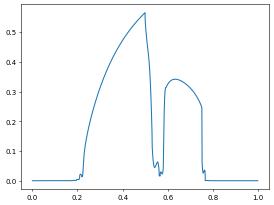
[27]:
from dune.fem.function import levelFunction
@gridFunction(gridView=grid,name="polOrder",order=0)
def polOrder(e,x):
return [spc.localOrder(e)]
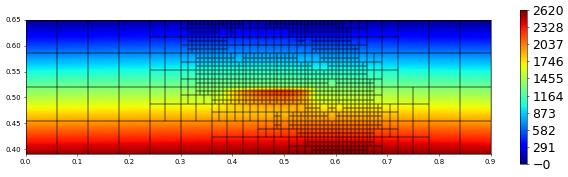
plot(solution[0],figsize=(15,4))
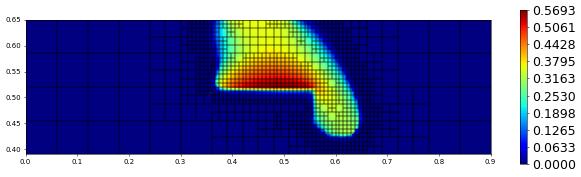
plot(solution[1],figsize=(15,4))
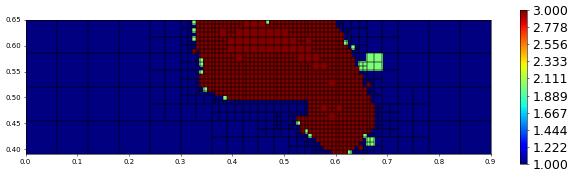
plot(polOrder,figsize=(15,4))
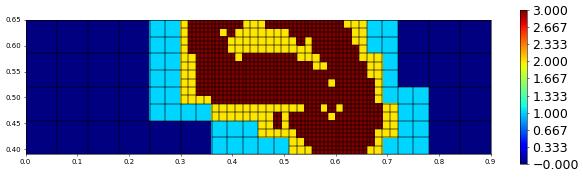
plot(levelFunction(grid),figsize=(15,4))
Note
This document is part of the dune-fem tutorialJupyter notebook (.ipynb) or as Python script (.py)