Cahn-Hilliard
In this script we show how to use the \(C^1\) non-conforming virtual element space to solve the Cahn-Hilliard equation. We use a fully implicit scheme here. You can find more details in [DH21]
[1]:
try:
import dune.vem
except:
print("This example needs 'dune.vem' - skipping")
import sys
sys.exit(0)
from matplotlib import pyplot
import random
from dune.grid import cartesianDomain, gridFunction
import dune.fem
from dune.fem.plotting import plotPointData as plot
from dune.fem.function import discreteFunction
from ufl import *
import dune.ufl
dune.fem.threading.use = 4
Grid and space construction - we use a cube grid here:
[2]:
order = 3
polyGrid = dune.vem.polyGrid( cartesianDomain([0,0],[1,1],[30,30]), cubes=True)
testSpaces = [ [0], [order-3,order-2], [order-4] ]
# testSpaces = [ [0,0],[order-4,order-3], [order-4] ]
space = dune.vem.vemSpace(polyGrid, order=order, testSpaces=testSpaces)
To define the mathematical model, let \(\psi\colon{\mathbb R} \rightarrow \mathbb{R}\) be defined as \(\psi(x) = \frac{(1-x^2)^2}{4}\) and let \(\phi(x) = \psi(x)^{\prime}\). The strong form for the solution \(u\colon \Omega \times [0,T] \rightarrow {\mathbb R}\) is given by \begin{align*} \partial_t u - \Delta (\phi(u)-\epsilon^2 \Delta u) = 0 \quad &\text{in} \ \Omega \times [0,T] ,\\ u(\cdot,0) = u_0(\cdot) \quad &\text{in} \ \Omega,\\ \partial_n u = \partial_n \big( \phi(u) - \epsilon^2\Delta u \big) = 0 \quad &\text{on} \ \partial \Omega \times [0,T]. \end{align*}
We use a backward Euler discretization in time and will fix the constant further down:
[3]:
t = dune.ufl.Constant(0,"time")
tau = dune.ufl.Constant(0,"dt")
eps = dune.ufl.Constant(0,"eps")
df_n = discreteFunction(space, name="oldSolution") # previous solution
x = SpatialCoordinate(space)
u = TrialFunction(space)
v = TestFunction(space)
H = lambda v: grad(grad(v))
laplace = lambda v: H(v)[0,0]+H(v)[1,1]
a = lambda u,v: inner(H(u),H(v))
b = lambda u,v: inner( grad(u),grad(v) )
W = lambda v: 1/4*(v**2-1)**2
dW = lambda v: (v**2-1)*v
equation = ( u*v + tau*eps*eps*a(u,v) + tau*b(dW(u),v) ) * dx == df_n*v * dx
dbc = [dune.ufl.DirichletBC(space, 0, i+1) for i in range(4)]
# energy
Eint = lambda v: eps*eps/2*inner(grad(v),grad(v))+W(v)
Next we construct the scheme providing some suitable expressions to stabilize the method
[4]:
biLaplaceCoeff = eps*eps*tau
diffCoeff = 2*tau
massCoeff = 1
scheme = dune.vem.vemScheme(
[equation, *dbc],
solver=("suitesparse","umfpack"),
hessStabilization=biLaplaceCoeff,
gradStabilization=diffCoeff,
massStabilization=massCoeff,
boundary="derivative") # only fix the normal derivative = 0
To avoid problems with over- and undershoots we project the initial conditions into a linear lagrange space before interpolating into the VEM space:
[5]:
def initial(x):
h = 0.01
g0 = lambda x,x0,T: conditional(x-x0<-T/2,0,conditional(x-x0>T/2,0,sin(2*pi/T*(x-x0))**3))
G = lambda x,y,x0,y0,T: g0(x,x0,T)*g0(y,y0,T)
return 0.5*G(x[0],x[1],0.5,0.5,50*h)
initial = dune.fem.space.lagrange(polyGrid,order=1).interpolate(initial(x),name="initial")
df = space.interpolate(initial, name="solution")
Finally the time loop:
[6]:
t.value = 0
eps.value = 0.05
tau.value = 1e-02
fig = pyplot.figure(figsize=(40,20))
count = 0
pos = 1
while t.value < 0.8:
df_n.assign(df)
info = scheme.solve(target=df)
t.value += tau
count += 1
if count % 10 == 0:
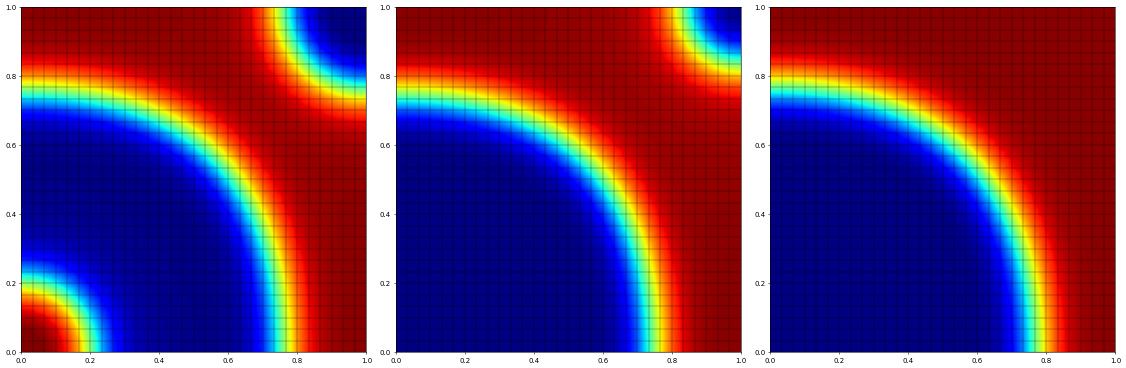
df.plot(figure=(fig,240+pos),colorbar=None,clim=[-1,1])
energy = dune.fem.integrate(Eint(df),order=3)
print("[",pos,"]",t.value,tau.value,energy,info,flush=True)
pos += 1
[ 1 ] 0.09999999999999999 0.01 0.21102453532933635 {'converged': True, 'iterations': 2, 'linear_iterations': 2, 'timing': [0.504231952, 0.32584044700000003, 0.178391505]}
[ 2 ] 0.20000000000000004 0.01 0.1994091755313673 {'converged': True, 'iterations': 3, 'linear_iterations': 3, 'timing': [0.72588597, 0.482899321, 0.242986649]}
[ 3 ] 0.3000000000000001 0.01 0.15197040274213286 {'converged': True, 'iterations': 3, 'linear_iterations': 3, 'timing': [0.737873117, 0.49538051699999996, 0.24249260000000006]}
[ 4 ] 0.4000000000000002 0.01 0.13249947516990448 {'converged': True, 'iterations': 3, 'linear_iterations': 3, 'timing': [0.725629579, 0.483352676, 0.24227690300000004]}
[ 5 ] 0.5000000000000002 0.01 0.11180986038851853 {'converged': True, 'iterations': 3, 'linear_iterations': 3, 'timing': [0.726114539, 0.48388029600000004, 0.24223424299999996]}
[ 6 ] 0.6000000000000003 0.01 0.1091060094198979 {'converged': True, 'iterations': 2, 'linear_iterations': 2, 'timing': [0.491215455, 0.321909899, 0.16930555600000002]}
[ 7 ] 0.7000000000000004 0.01 0.10659833564947833 {'converged': True, 'iterations': 2, 'linear_iterations': 2, 'timing': [0.491623948, 0.32167951000000006, 0.16994443799999992]}
[ 8 ] 0.8000000000000005 0.01 0.10398570727025969 {'converged': True, 'iterations': 2, 'linear_iterations': 2, 'timing': [0.508835881, 0.34074715899999997, 0.16808872200000002]}
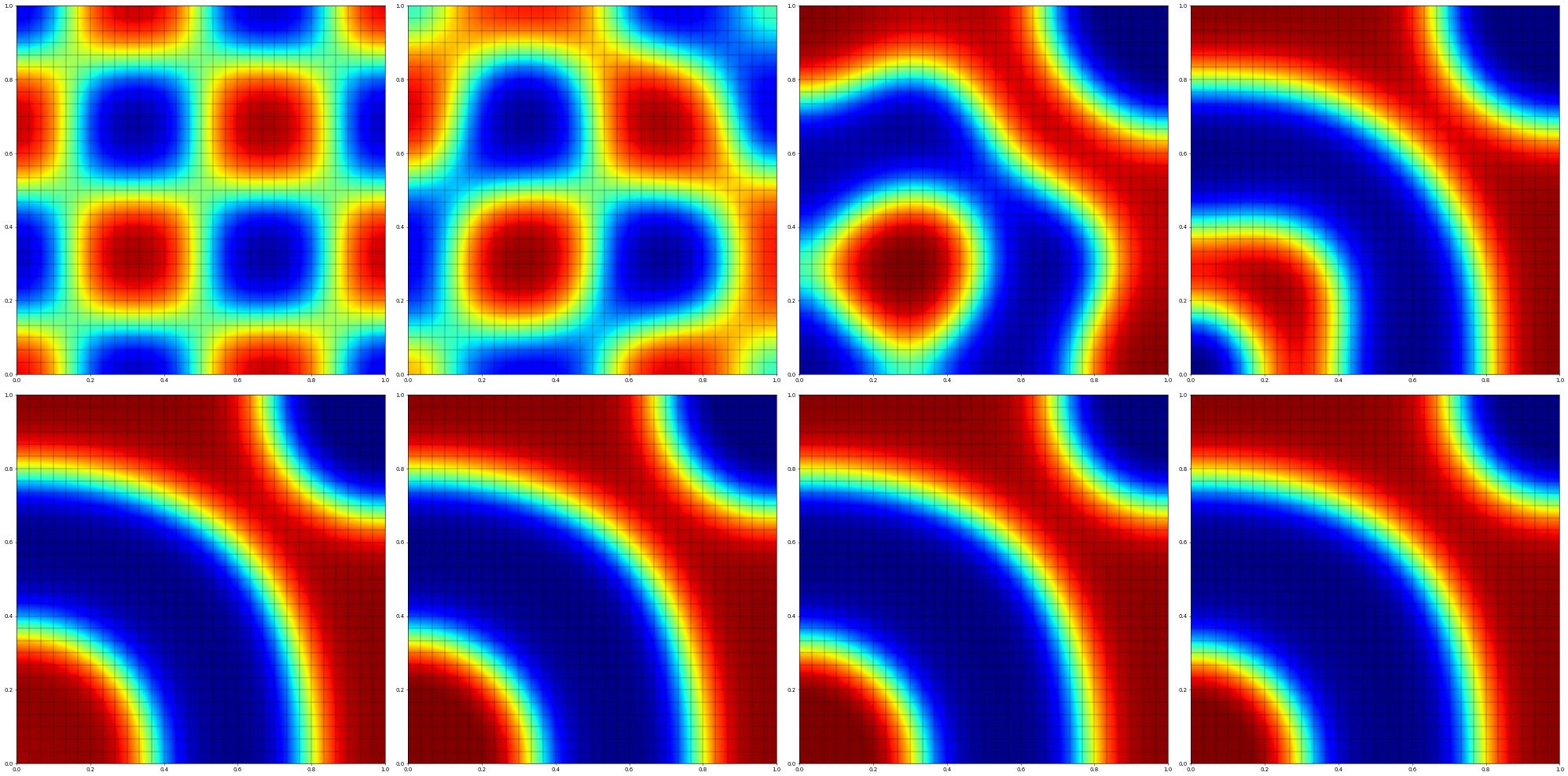
For the final coarsening phase we increase the time step a bit:
[7]:
tau.value = 4e-02
fig = pyplot.figure(figsize=(30,10))
count = 0
pos = 1
while t.value < 2.0:
df_n.assign(df)
info = scheme.solve(target=df)
t.value += tau
count += 1
if count % 10 == 0:
df.plot(figure=(fig,140+pos),colorbar=None,clim=[-1,1])
energy = dune.fem.integrate(Eint(df),order=3)
print("[",pos,"]",t.value,tau.value,energy,info,flush=True)
pos += 1
[ 1 ] 1.2000000000000008 0.04 0.09159602767486563 {'converged': True, 'iterations': 3, 'linear_iterations': 3, 'timing': [0.721659909, 0.48155142400000006, 0.24010848499999993]}
[ 2 ] 1.6000000000000012 0.04 0.07005804064896495 {'converged': True, 'iterations': 3, 'linear_iterations': 3, 'timing': [0.742393265, 0.489710215, 0.25268305]}
[ 3 ] 2.0000000000000013 0.04 0.05881699202557058 {'converged': True, 'iterations': 2, 'linear_iterations': 2, 'timing': [0.502380104, 0.325223115, 0.177156989]}
This page was generated from
the notebook chimpl_nb.ipynb
and is part of the tutorial for the dune-fem python bindings
