|
| template<class Intersection , class Point > |
| void | linearizedRobinFlux (const RangeType &uBar, const Intersection &intersection, const Point &x, const DomainType &unitOuterNormal, const RangeType &value, RangeType &result) const |
| | The linearized Robin-type flux term. More...
|
| |
| void | setEntity (const Entity &entity) const |
| |
| void | flux (const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, JacobianRangeType &flux) const |
| |
| void | linearizedFlux (const RangeType &uBar, const JacobianRangeType &DuBar, const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, JacobianRangeType &flux) const |
| |
| void | source (const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, RangeType &result) const |
| |
| void | linearizedSource (const RangeType &uBar, const JacobianRangeType &DuBar, const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, RangeType &result) const |
| |
| void | robinFlux (const Intersection &intersection, const Point &x, const DomainType &unitOuterNormal, const RangeType &value, RangeType &result) const |
| |
| void | fluxDivergence (const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, const HessianRangeType &hessian, RangeType &result) const |
| |
|
const ExpressionType & | expression () const |
| | Return a const reference to the underlying expression.
|
| |
|
ExpressionType & | expression () |
| | Return a mutable reference to the underlying expression.
|
| |
|
ExpressionType | operator* () const |
| | Return a copy from of the underlying expression.
|
| |
template<class FunctionSpace, class Indicator = EntireBoundaryIndicatorType>
class Dune::ACFem::RobinBoundaryOperatorParts< FunctionSpace, Indicator >
A (homogeneous) Robin-boundary model.
(linear) Robin boundary-conditions are in general boundary conditions of the following form
\[
(A(x)\nabla u(x))\cdot\nu(x) = c(x)\,(u^{\text{ext}}(x) - u(x))\text{ on }\Gamma_R
\]
where \(A(x)\) is the coefficient matrix of the principle part of an associated PDE of 2nd order, \(c(x)\) is a given wnon-negative cofficient function and \(u^{\text{ext}}(x)\) is some given function.
This models the scenario that the flux of the qunatity u over the boundary is proportional to the difference to some prescribed external temperature distribution with transition coefficient \(c(x)\).
This particular model implements the following homogeneous special case:
\[
(A(x)\nabla u(x))\cdot\nu(x) = - u(x))\text{ on }\Gamma_R
\]
The general non-homogeneous case with arbitrary coefficient function can be obtained by subtracting the inhomogeneity from the model and multiplying the resulting non-homogeneous Robin-model with transition coefficent 1 by the desired transition coefficent, which may be a constant, parameter of function.
- Parameters
-
| [in] | Indicator | The boundary indicator function which decides on which part of the boundary the Robin boundary conditions is imposed. |
- Note
- Note also that the inhomogeneity uExt is internally incorporated into the Neumann boundary data.
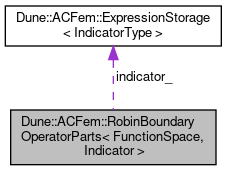
 Collaboration diagram for Dune::ACFem::RobinBoundaryOperatorParts< FunctionSpace, Indicator >:
Collaboration diagram for Dune::ACFem::RobinBoundaryOperatorParts< FunctionSpace, Indicator >: |
Legal Statements / Impressum |
Hosted by TU Dresden & Uni Heidelberg |
generated with Hugo v0.111.3
(Sep 3, 22:42, 2025)
|
Legal Statements / Impressum |
Hosted by TU Dresden & Uni Heidelberg |
generated with Hugo v0.111.3
(Sep 3, 22:42, 2025)