|
| template<class Entity , class Point > |
| void | flux (const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, JacobianRangeType &flux) const |
| | Evaluate \(A(x, u)\nabla u(x)\) in local coordinates. More...
|
| |
| template<class Entity , class Point > |
| void | linearizedFlux (const RangeType &uBar, const JacobianRangeType &DuBar, const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, JacobianRangeType &flux) const |
| | Evaluate the linearized flux in local coordinates. More...
|
| |
| template<class Entity , class Point > |
| void | fluxDivergence (const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, const HessianRangeType &hessian, RangeType &result) const |
| | Compute the point-wise value of the flux-part of the operator, meaning the part of the differential operator which is multiplied by the derivative of the test function. More...
|
| |
| void | setEntity (const Entity &entity) const |
| |
| bool | setIntersection (const Intersection &intersection) const |
| |
| void | source (const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, RangeType &result) const |
| |
| void | linearizedSource (const RangeType &uBar, const JacobianRangeType &DuBar, const Entity &entity, const Point &x, const RangeType &value, const JacobianRangeType &jacobian, RangeType &result) const |
| |
| void | robinFlux (const Intersection &intersection, const Point &x, const DomainType &unitOuterNormal, const RangeType &value, RangeType &result) const |
| |
| void | linearizedRobinFlux (const RangeType &uBar, const Intersection &intersection, const Point &x, const DomainType &unitOuterNormal, const RangeType &value, RangeType &result) const |
| |
|
const ExpressionType & | expression () const |
| | Return a const reference to the underlying expression.
|
| |
|
ExpressionType & | expression () |
| | Return a mutable reference to the underlying expression.
|
| |
|
ExpressionType | operator* () const |
| | Return a copy from of the underlying expression.
|
| |
template<class FunctionSpace, class Parameter = TrivialParameter<typename FunctionSpace::RangeType>>
class Dune::ACFem::MeanCurvatureOperatorParts< FunctionSpace, Parameter >
Define a mean-curvature model for graphs and level-sets.
This model implements the bulk-term
\[
\int_\Omega \frac{\nabla u\cdot\nabla\phi}{\sqrt{\eta^2+|\nabla u|^2}}
\]
The linearization at \(\bar u\) reads
\[
\int_\Omega
\frac{\nabla u\cdot\nabla\phi}{\sqrt{\eta^2+|\nabla \bar u|^2}}
-
\frac{(\nabla \bar u\cdot\nabla u)\,(\nabla \bar u\cdot\nabla\phi)}{\sqrt{\eta^2+|\nabla \bar u|^2}^3}
\]
The divergence of the flux term is
\[
-\nabla\cdot\frac{\nabla u}{\sqrt{\eta^2+|\nabla u|^2}}
=
-\frac{\Delta u}{\sqrt{\eta^2+|\nabla u|^2}}
+
\frac{(\nabla u)^T (\nabla^2 u)\nabla u}{\sqrt{\eta^2+|\nabla u|^2}^3}
\]
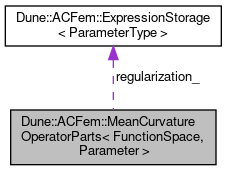
 Collaboration diagram for Dune::ACFem::MeanCurvatureOperatorParts< FunctionSpace, Parameter >:
Collaboration diagram for Dune::ACFem::MeanCurvatureOperatorParts< FunctionSpace, Parameter >: |
Legal Statements / Impressum |
Hosted by TU Dresden & Uni Heidelberg |
generated with Hugo v0.111.3
(Sep 3, 22:42, 2025)
|
Legal Statements / Impressum |
Hosted by TU Dresden & Uni Heidelberg |
generated with Hugo v0.111.3
(Sep 3, 22:42, 2025)