dune-tpmc

dune-tpmc (dune-tpmc)

Provides a topology preserving implementation of the marching cubes and marching simplex algorithm. This module can be used to implement cut-cell algorithms on top of the Dune interface.

Requires:	dune-common
Maintainer:	Christian Engwer, Andreas Nüßing
Git repository:	https://gitlab.dune-project.org/extensions/dune-tpmc

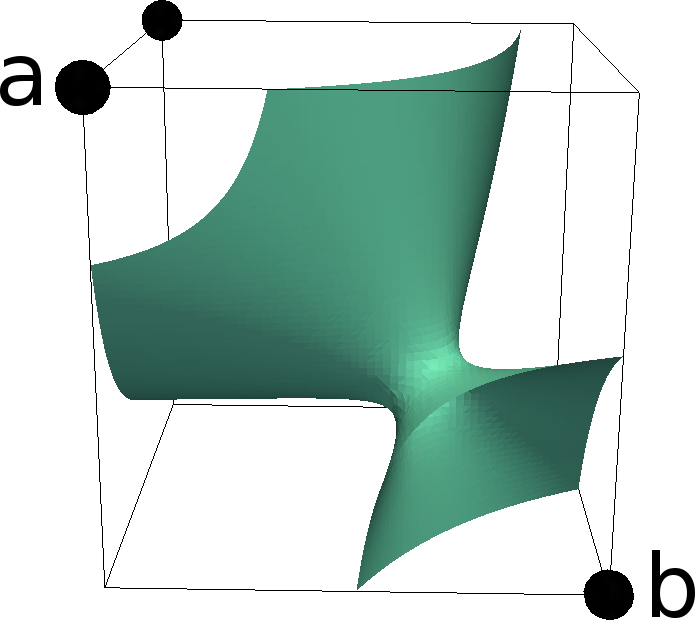
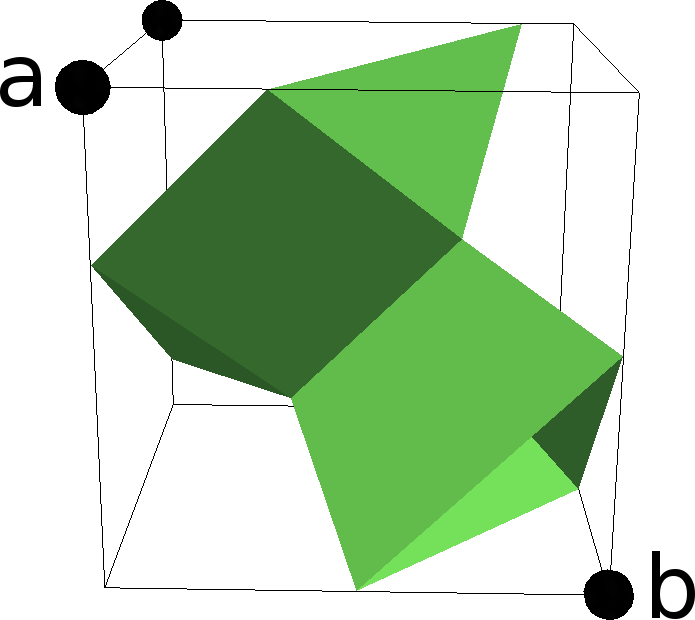
Given a scalar P1/Q1 function Φ on a domain Ω, we define a partition of Ω into two sub-domains {Ω1, Ω2} with a common interface Γ. The interface is given as the zero level-set of the scalar function Φ. The marching cubes algorithm computes a piece-wise linear reconstruction of Γ.

The dune-tpmc modules not only computes a reconstruction of the interface, but also further information. The user can access the following information:

• Reconstruction of the interface Γ
• Reconstruction of Ω1
• Reconstruction of Ω2
• Connectivity pattern w.r.t. each sub-domain

In order to allow the algorithm to be employed in Finite Element simulations, a reconstruction has to fulfill certain topological guarantees:

• The connectivity pattern of the cell vertices must be preserved within each subentity. In particular this means that vertices connected along an edge, face or volume, should still be connected via the same subentity.
• The exact interface Γ partitions each grid cell into patches belonging to either Ω1 or Ω2. We require that number of patches and their domain association is the same in the polygonal reconstruction.
• The vertices of the reconstructed interface lie on the exact zero level-set.

Publications and Documentation

If you are using the dune-tpmc module, please cite

The first concepts of dune-tpmc go back to implementations described in

• Ch. Engwer, An Unfitted Discontinuous Galerkin Scheme for Micro-scale Simulations and Numerical Upscaling, Heidelberg University, 2009. (PDF)

Installation

dune-tpmc depends on the TPMC library for generating of the lookup-tables.

You can install TPMC via pip. Currently it is not listed in the pypi repository and must be installed directly from the github repository:

• for python 2:

> python -m pip install git+https://github.com/tpmc/tpmc.git

• for python 3 we have preliminary support:

> python -m pip install git+https://github.com/tpmc/tpmc.git@python3

Maintainers

dune-tpmc has been written by Christian Engwer and Andreas Nüßing.