Reference Elements

Classes
struct	Dune::ReferenceElements< ctype, dim >
	Class providing access to the singletons of the reference elements. More...
class	Dune::ReferenceElement< ctype, dim >
	This class provides access to geometric and topological properties of a reference element. More...

Detailed Description

Generic Geometries

Introduction

In the following we will give a definition of reference elements and subelement numbering. This is used to define geometries by prescribing a set of points in the space \( \mathbf{R}^w \).

The basic building block for these elements is given by a recursion formula which assigns to each set \( E \subset \mathbf{R}^d \) either a prism element \( E^\vert\subset \mathbf{R}^{d+1} \) or a pyramid element \( E^\circ\subset \mathbf{R}^{d+1} \) with \( E^\vert = \lbrace (x,\bar{x}) \mid x \in E, \bar{x} \in [0,1] \rbrace \) and \( E^\circ = \lbrace ((1-\bar{x})x,\bar{x}) \mid x \in E, \bar{x} \in [0,1] \rbrace \). The recursion starts with a single point \( P_0=0\in\mathbf{R}^0 \).

For \( d=1,2,3 \) this leads to the following elements

• \( d=1 \): \( L_1 = P_0^\vert = P_0^\circ = [0,1] \) is a line.
• \( d=2 \): \( Q_2 = L_1^\vert \) is a cube and \( S_2 = L_1^\circ \) is a simplex.
• \( d=3 \): \( Q_3 = Q_2^\vert \) is a cube, \( S_3 = S_2^\circ \) is a simplex, \( \mathrm{pyramid}_3 = Q_2^\circ \) is a pyramid, and \( \mathrm{prism}_3 = S_2^\vert \) is a prism.

In general if \( Q_d \) is a cube then \( Q_d^\vert \) is also a cube and if \( S_d \) is a simplex then \( S_d^\circ \) is also a simplex.

Based on the recursion formula we can also define a numbering of the subentities and also of the sub-subentities of \( E^\vert \) or \( E^\circ \) based on a numbering of \( E \). For the subentities of codimension \( c \) we use the numbering

• \( E^\vert \): the first numbers are assigned to the entities parallel to the \( x_d-\)axis in the same order as the subentites of the same codimension in \( E \); then to the subentities of codimension \( c-1 \) in the bottom followed by those in the top.
• \( E^\circ \): in this case we first number the subentities of codimension \( c-1 \) in the bottom, followed by each subentity based on a subentity of codimension \( c \) in \( E \).

For the subentity of codimension \( cc \) in a codimension \( c \) subentity \( E' \) we use the numbering induced by the numbering the reference element corresponding to \( E' \).

Here is a graphical representation of the reference elements:

1. One-dimensional reference element. For d=1 the simplex and cube are identical
   
2. Two-dimensional reference simplex (a.k.a. triangle)
   
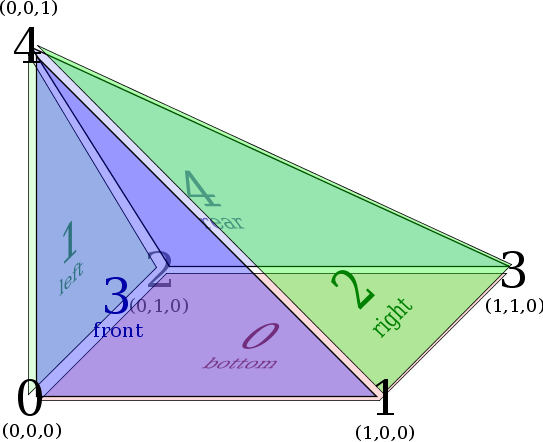
3. Three-dimensional reference simplex (a.k.a. tetrahedron)

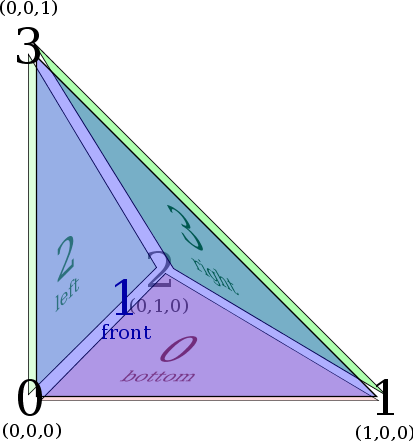   Face Numbering

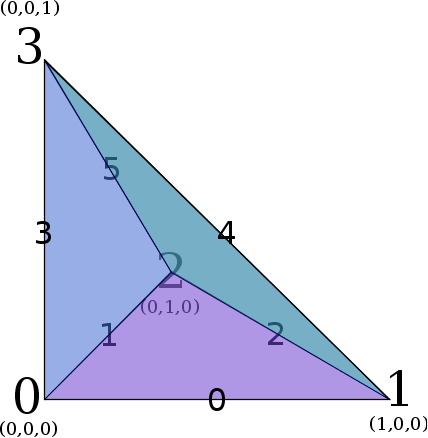   Edge Numbering

4. Two-dimensional reference cube (a.k.a. quadrilateral)
   
5. Three-dimensional reference cube (a.k.a. hexahedron)

   Face Numbering

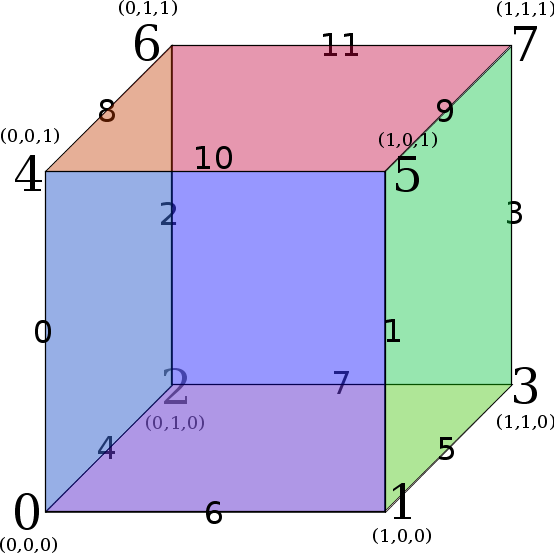   Edge Numbering

6. Prism reference element

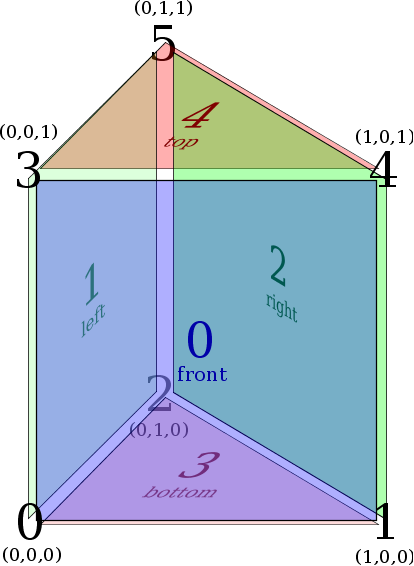   Face Numbering

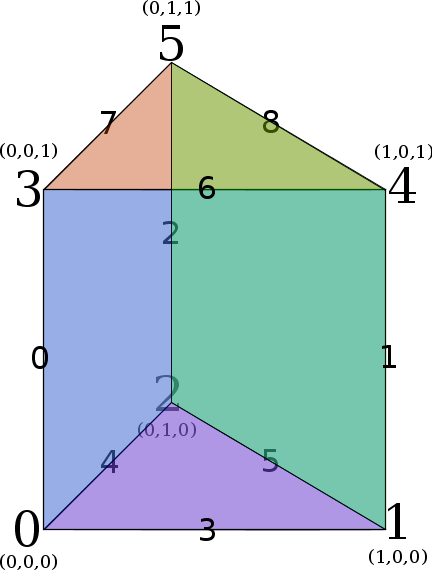   Edge Numbering

7. Pyramid reference element

   Face Numbering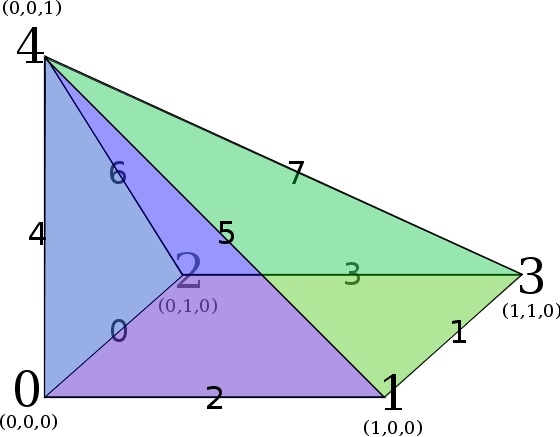

   Edge Numbering

In addition to the numbering and the corner coordinates of a reference element \( \hat{E} \) we also define the barycenters \( b(\hat{E}) \), the volume \( |\hat{E}| \) and the normals \( n_i(\hat{E}) \) to all codimension one subelements.

The recursion formula is also used to define mappings from reference elements \( E \) to general polytop given by a set of coordinates for the corner points - together with the mapping \( \Phi \), the transpose of the Jacobian \( D\Phi^T(x)\in\mathbf{R}^{d,w} \) is also defined where \( d \) is the dimension of the reference element and \( w \) the dimension of the coordinates. This suffices to define other necessary parts of a Dune geometry by LQ-decomposing \( D\Phi^T \): let \( D\Phi^T(x) = LQ \) be given with a lower diagonal matrix \( L\in \mathbf{R}^{d,d} \) and a matrix \( Q\in\mathbf{R}^{d,w} \) which satisfies \( Q Q^T = I \):

• Jacobian inverse transpose

  \[ D\Phi(x)^{-T}:=Q^T L^{-1}. \]

• Integration element

  \[ \sqrt{\mathrm{det}(D\Phi(x)^T D\Phi(x))} = \sqrt{\mathrm{det}(LL^T)} = \Pi_{i=1}^d l_{ii}. \]

• Volume

  \[ \int_{\hat{E}} \Pi_{i=1}^d l_{ii}(x) d\;x = |\hat{E}| \Pi_{i=1}^d l_{ii}(b(\hat{E})). \]

  (Here some assumptions on the degree of the integration element is used.)

The next sections describe the details of the construction.

Reference Topology

We define the set \(\mathcal{T}\) of reference topologies by the following rules:

• \(\mathcal{T}\) contains an element \(\mathbf{p}\) that we call the point topology.
• For \(T \in \mathcal{T}\), \(\mathcal{T}\) contains an element \(T^\vert\) that we call the prism over \(T\).
• For \(T \in \mathcal{T}\), \(\mathcal{T}\) contains an element \(T^\circ\) that we call the pyramid over \(T\).

For each reference topology \(T\) we define the following values:

• Dimension: The point topology has dimension zero and the dimension of a prism or a pyramid topology over \(t\) has dimension \(d(t)+1\).
• Size: For \(c=0,\dots,d\) with \(d=d(T)\) we define the number \(s_c(T)\) through
  • \(s_0(T)=1\).
  • If \(T=t^\vert\) then \(s_d(T)=2s_{d-1}(t)\) and for \(c\in \{1,\dots,d-1\}\) we have \(s_c(T)=s_{c}(t)+2s_{c-1}(t)\).
  • If \(T=t^\circ\) then \(s_d(T)=s_{d-1}(t)+1\) and for \(c\in \{1,\dots,d-1\}\) we have \(s_c(T)=s_{c-1}(t)+s_{c}(t)\).
• Subtopology: Given a reference topology \(T\) of dimension \(d\) and a codimension \(c=0,\dots,d\) we now define the subtopology \(S_{c,i}(T)\in\mathcal{T}\) for \(i=1,\dots,s_c(T)\):
  • \(S_{0,1}(T)=T\) and \(S_{d,i}(T)=\mathbf{p}\)
  • For \(T=t^\vert\) and \(c\in \{1,\dots,d-1\}\) we define using the abbreviations \(p=s_{c}(t),q=s_{c-1}(t)\)

    \[S_{c,i}(T) = \left\{\begin{array}{ll} S_{c,i}(t)^\vert & \mbox{for}\; i=1,\dots,p, \\ S_{c-1,i-p}(t) & \mbox{for}\; i=p+1,\dots,p+q, \\ S_{c-1,i-p-q}(t) & \mbox{for}\; i=p+q+1,\dots,p+2q. \end{array}\right. \]

  • For \(T=t^\circ\) and \(c\in \{1,\dots,d-1\}\) we define using the abbreviations \(p=s_{c}(t),q=s_{c-1}(t)\)

    \[S_{c,i}(T) = \left\{\begin{array}{ll} S_{c-1,i}(t) & \mbox{for}\; i=1,\dots,q, \\ S_{c,i-q}(t)^\circ & \mbox{for}\; i=q+1,\dots,q+p. \end{array}\right. \]

Notice that the number of vertices (i.e., subtopologies of codimension \(d(T)\)) of a topology \(T\) does not uniquely identify the topology. To see this, consider the topologies \(T_1 = \mathbf{p}^{\vert\vert\vert\circ\circ}\) and \(T_2 = \mathbf{p}^{\circ\circ\circ\circ\vert}\). For these topologies we have \(s_d( T_1 ) = s_d( T_2 ) = 10\).

Reference Domains

For each reference topology \(T\) we assosiate the set of corners \(\mathcal{C}(T):=(p_i(T))_{1=1}^{s_d(T)}\subset\mathbf{R}^d(T)\) defined through

• \(T=\mathbf{p}\): \(p_0(T)=0\in\mathbf{R}^0\)
• \(T=t^\vert\): \(p_k(T)=(p_k(t),0),p_{d'+k}(T)=(p_k(t),1)\) for \(k=1,\dots,d'\), with \(d'=s_d(t)\).
• \(T=t^\circ\): \(p_k(T)=(p_k(t),0)\) for \(k=1,\dots,d-1\) and \(p_d(T)=e_d\) with \(d=s_d(T)\)

The convex hall of the set of points \(\mathcal{C}(T)\) defines the reference domain \(\mathrm{domain}(T)\) for the reference topology \(T\); it follows that

• \(\mathrm{domain}( \mathbf{p} ) := \lbrace 0 \rbrace \subset \mathbf{R}^0\),
• \(\mathrm{domain}( T^\vert ) := \mathrm{domain}( T ) \times [0,1]\),
• \(\mathrm{domain}( T^\circ ) := \lbrace ((1-\bar{x})x,\bar{x}) \mid x \in \mathrm{domain}( T ), \bar{x} \in [0,1] \rbrace\).

Reference Elements and Mappings

A pair \(E=(T,\Phi)\) of a topology \(T\) and a map \(\Phi:\mathrm{domain}( T ) \to \mathbf{R}^w\) with \(w\geq d(T)\) is called an element.

The reference element is the pair \(E(T)=(T,{\rm id})\).

For a given set of points \(\mathcal{C}:=(p_i)_{1=1}^{s_d(T)}\subset\mathbf{R}^w\) we define a mapping \(\Phi_T(\mathcal{C},\cdot)\mathrm{domain}( T ) \to \mathbf{R}^w\) through \(\Phi_T(\mathcal{C};p_i(T))=p_i\) for all \(p_i(T)\in \mathcal{C}(T)\). This mapping can be expressed using the recursive definition of the reference topologies through:

• \(\Phi_{\mathbf{p}}( (p_0) ; x ) = p_0\),
• \(\Phi_{T^\vert}( (p_1,\ldots,p_{s_d(T^\vert)} ; (x,\bar{x}) ) = (1 - \bar{x}) \Phi_T( p_1,\ldots,p_{s_d(T)} ; x ) + \bar{x} \Phi_T( p_{s_d(T)+1},\dots,p_{s_d(T^\vert)} ; x )\) with \(x\in \mathrm{domain}( T )\) and \(\bar{x}\in[0,1]\).
• \(\Phi_{T^\circ}( p_1,\ldots,p_{s_d(T^\circ)}) ; (x,\bar{x}) ) = (1 - \bar{x}) \Phi_T( p_1,\ldots,p_{s_d(T)-1} ; x ) + \bar{x} p_{s_d(T^\circ)} \) with \(x\in \mathrm{domain}( T )\) and \(\bar{x}\in[0,1]\).

Numbering of Subelements

Given a reference topology \(T\), a codimension \(c\in\{0,\dots,d(T)\}\) and a subtopology \(S_{c,i}(T)\) we define a subset of the corner set \(\mathcal{C}(T)\) \( \mathcal{C}_{c,i}(T)= (p_{k_j}(T))_{j=1}^{s_{d(S_{c,i}(T)}(S_{c,i}(T))} \) given by the subsequence \( \mathcal{K}_{c,i}(T)=(k_j)_{j=1}^{s_{d(S_{c,i}(T)}(S_{c,i}(T))} \) of \( \{1,dots,s_{d(T)}(T)\} \):

\( \mathcal{C}_{0,0}(T) = \mathcal{C}(T)\), \( \mathcal{C}_{d(T),i}(T) = (p_i(T)) \), and for \(c\in\{1,\dots,d(T)-1\}\) we define \( \mathcal{K}_{c,i}(T)=(k_j)_{j=1}^{s_{d(S_{c,i}(T)}(S_{c,i}(T))} \) through the recursion

• \(T=t^\vert\):
  For \( i=1,\dots,s_c(T) \) we define \( \mathcal{K}_{c,i}(T)=(k_1,\dots,k_n, k_1+s_{d(t)}(t)\dots,k_n+s_{d(t)}(t)) \) with \( \mathcal{K}_{c,i}(T)= \{k_1,\dots,k_n\} \).
  For \( i=s_(T)+1,\dots,s_c(T)+s_{c+1}(T) \) we define \( \mathcal{K}_{c,i}(T)=(k_1,\dots,k_n) \) with \( \mathcal{K}_{c-1,i}(T)= \{k_1,\dots,k_n\} \).
  For \( i=s_c(T)+s_{c+1}(T)+1,\dots,s_c(T)+2s_{c+1}(T) \) we define \( \mathcal{K}_{c,i}(T)=(k_1+s_{d(t)}(t),\dots,k_n+s_{d(t)}(t)) \) with \( \mathcal{K}_{c-1,i}(T)= \{k_1,\dots,k_n\} \).
• \(T=t^\circ\):
  For \( i=1,\dots,s_{c-1}(T) \) we define \( \mathcal{K}_{c,i}(T)=(k_1,\dots,k_n) \) with \( \mathcal{K}_{c-1,i}(T)= \{k_1,\dots,k_n\} \).
  For \( i=s_{c-1}(T)+1,\dots,s_{c-1}(T)+s_c(T) \) we define \( \mathcal{K}_{c,i}(T)=(k_1,\dots,k_n,s_{d(T)}(T)) \) with \( \mathcal{K}_{c-1,i}(T)= \{k_1,\dots,k_n\} \).

Given these subsets we define subreference elements \(E_{c,i}(T)=(S_{c,i}(T),\Phi_{c,i}(T))\) of \(E(T)\) given by the following mapping \( \Phi_{c,i}(T,\cdot)=\Phi(S_{c,i}(T),\mathcal{C}_{c,i}(T),\cdot) \).

Furthermore we define a numbering of the subreference elements of each subreference element in \(T\). This is the number \( k=\mathrm{index}_{c,i,cc,ii}(T)\) for \(c\in\{0,\dots,d(T)\}\), \( i\in\{1,\dots,s_c(T)\} \), and \( cc\in\{0,\dots,d(S_{c,i})\}\), \( ii\in\{1,\dots,s_{cc}(S_{c,i})\} \) for which

\[\Phi_{c,i}(S_{c,i}(T))\circ \Phi_{cc,ii}(S_{cc,ii}(S_{c,i}(T))) = \Phi_{c+cc,k}(T).\]